In the following we will discuss the gradient of the dipole gravity potential. This shows the detailed picture of the actual force associated with dipole gravity. This program is accomplished by taking the gradient in the spherical coordinate system on the isolated dipole potential.
where the function f is replaced by the following expression which is the total gravity, ie, the Newtonian gravity plus the dipole gravity for a rotating hemisphere.

In the case of the radial component(r dependent force) of the dipole gravity force, 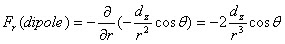 ,
,
where dz is the gravitational dipole moment and the latitude angle theta is measured from positive Z axis of the rotation. Since the center of mass moves toward the flat side of the hemisphere while in rotation, convention has to be made in such a way that the flat side of the hemisphere faces the positive Z axis.
The value of the cosine function changes its sign from positive to negative as it crosses over the equatorial plane of the rotating hemisphere, which is located at half the length of the radius down from the flat side of the hemisphere toward the dome, where the latitude angle is 90 degree.
This is the fundamental cause of the repulsive gravity force at the domed side of the rotating hemisphere and the unidirectional acceleration of the isolated dipole gravitational moment in the matter filled universe and also the justification for the experiments proposed in
http://dipoleantigravity.blogspot.com/2007/04/alternative-method-of-detecting-dipole.html
and
http://dipoleantigravity.blogspot.com/2007/04/testable-prediction-from-rotating.html.
It must be noted that this is the same force that produces the Lens-Thirring force near the center of the rotating sphere when the two rotating hemispheres are superposed face to face to form a single rotating sphere.
The latitude angular dependency of the dipole gravity force 
is represented by the force in the direction from the flat side of the poles toward the domed side following the latitude circular curvature of the radius r. The strength of it is maximum at the equatorial plane which is at the 90 degree latitude angular position and it is minimum when the latitude angle is either at zero or 180 degree.
At this point, it must be noted that the directions of the force lines resemble exactly that of a dipole bar magnet. In all the similarities and qualifications, this is the gravitational dipole magnet as stated in the introduction, the true "gravito-magnetism" that has been searched for a long time.
After all those effects and calculations, there is one new physical entity stands out, that is this new negative gravitational mass pole on the domed side of the rotating hemisphere which exists temporarily with the angular momentum. Since the angular momentum is conserved, the negative mass pole doesn't disappear as long as the angular momentum stays on. It can also be seen that this negative gravitational mass pole can not exist in the universe in isolation.
The last phi(circumferential angle) directional dipole gravity force is zero because there is no phi dependency in the dipole gravity potential.
We don't know exactly what it means when people say "frame dragging force" in terms of its mathematical form, but at least there is no "dragging" force that follows the rotating surface along the circumferential direction(phi direction) within dipole gravity which is the strongest gravity force next to the Newtonian monopole force.
This term is normally used in association with Lens-Thirring force but its strength is v/c times smaller compared to the radial dipole gravity force. Lens-Thirring force is certainly a part of gravito-magnetism(dipole gravity) but "frame dragging force" is too weak(V/c) to be a part of it. If Gravity Probe B works perfectly, it will detect dipole effect in a much more stronger signal before it detects the "frame dragging" force.
No comments:
Post a Comment